Trigonometry in the CAT exam is a broad topic. However, that doesn’t imply direct questions will appear in the exam from this topic. Mostly, trigonometric concepts appear in relation to geometric problems in the Quantitative Aptitude Section. The questions in relation to Trigonometric concepts appear in relation to other related concepts in the Quant section.

Most students often overlook these basic concepts. This causes them to forget the basics and results in losing points. Consequently, this results in an unsatisfactory overall CAT percentile. That’s why our CAT coaching has compiled this article to help you study important trigonometric basics in less than 7 minutes. In this article, we will discuss concepts, basic formulas and some examples in brief.

Basic Trigonometric Concepts

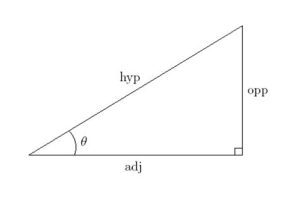
The fundamental concept in trigonometry is based on ratios of the angles in a triangle. These ratios are Trigonometric ratios.

There are six Trigonometric ratios. Each fundamental trigonometric ratio is unique.

Let’s consider the above triangle as ABC.

So, AC = Hypotenuse of the triangle

AB = Adjacent side to the Angle θ

BC = Opposite side to Angle θ

Then, the trigonometric ratios are

• Sin θ = Sine of angle θ = (Opposite side to Angle θ)/(Hypotenuse of the Triangle) = (BC/AC)
• Cos θ = Cosine of angle θ = (Adjacent side to Angle θ)/(Hypotenuse of the Triangle) = (AB/AC)
• Tan θ = Tangent of angle θ = (Opposite side to Angle θ)/(Adjacent side to Angle θ) = (BC/AB)
• Cot θ = Cotangent of angle θ = (Adjacent side to Angle θ)/(Opposite side to Angle θ) = (AB/BC)
• Sec θ = Secant of angle θ = (Hypotenuse of the Triangle)/(Adjacent side to Angle θ) = (AC/AB)
• Cosec θ = Cosecant of angle θ = (Hypotenuse of the Triangle)/(Opposite side to Angle θ) = (AC/BC)

Trigonometric ratios with respect to Angles:

These trigonometric ratios of some specific angles are widely used in numerous mathematical problems. Simultaneously, these ratios are easy to remember as well as they follow a certain discernible pattern.

Angle θ / Ratio	0°	30°	45°	60°	90°
Sin θ	0	1/2	1/ 21/2	31/2 /2	1
Cos θ	1	31/2 /2	1/ 21/2	1/2	0
Tan θ	0	1/31/2	1	31/2	Not Defined
Cot θ	Not Defined	31/2	1	1/31/2	0
Sec θ	1	2/31/2	21/2	2	Not Defined
Cosec θ	Not Defined	31/2	1	1/31/2	0

Basic Identities and Formulae:

Trigonometric ratios of complementary angles:

• Sin (90° − θ) = Cos θ
• Cos (90° − θ) = Sin θ
• Tan  (90° − θ) = Cot θ
• Cot (90° − θ) = Tan θ
• Sec (90° − θ) = Cosec θ
• Cosec (90° − θ) = Sec θ

Trigonometric Identities:

• Sin² θ + Cos² θ = 1
• Tan² θ + 1 = Sec² θ
• Cot² θ + 1 = Cosec² θ

Special Triangles’ Ratio:

There are two triangles that have the same trigonometric ratio value regardless of the length of their sides. These two triangles have sides with angles 45°-45°-90° and 30°-60°-90°.

In a 45°-45°-90° triangle, the ratio of sides, are 1:1:2^½  respectively.

In a 60°-30°-90° triangle, the ratio of sides are 1:3^½:2 respectively.

Example Questions:

1.  In a triangle ABC, if Sin A, Sin B, Sin C are sines of angles A, B, C respectively, then a Sin (B − C) + b Sin ( C − A) + c Sin (A − B) =

Options:

(a) 0

(b) 1

(c) 2

(d) None

Solution:

Given,

in triangle ABC,

let’s assume that

a/Sin A = b/Sin B = c/Sin C = K

then,

a = k Sin A,

b = k Sin B

c = k Sin C

Now consider the equation given which is

⇒ a Sin (B − C) + b Sin (C − A) + c Sin (A − B)

Substitute the values of a, b, c in the above equation

= k Sin A (Sin B Cos C −Cos B Sin C) + k Sin B (Sin C Cos A − Cos C Sin A) + k Sin C (Sin A Cos B − Cos A Sin B)

=k Sin A (Sin B Cos C − Cos B Sin C) + k Sin B (Sin C Cos A − Cos C Sin A) + k Sin C (Sin A Cos B − Cos A Sin B)

= k Sin A Sin B Cos C − k Sin A Cos B Sin C + k Sin B Sin C Cos A −k Sin B Cos C Sin A + k Sin C Sin A Cos B − k Sin C Cos A Sin B

= 0

Hence, the correct option is (a)

 

2. If Cos A + Cos² A = 1 and a Sin¹² A + b Sin¹⁰ A + c Sin⁸  A + d Sin⁶  A − 1 = 0. Find the value of a+(b/c)+d

Options:

(a) 4

(b) 3

(c) 6

(d) 1

Solution:

Given,

Cos A = 1 − Cos² A

Cos A = Sin² A

Square on both sides

Then, Cos²A = Sin⁴ A

1 − Sin² A = Sin⁴ A

1 = Sin⁴ A + Sin² A

Cube on both sides

1³  = (Sin⁴ A + Sin² A)³

1 = Sin¹² A + Sin⁶ A + 3Sin⁸ A + 3Sin¹⁰ A

Sin¹² A + Sin⁶ A + 3Sin⁸ A +3Sin¹⁰ A − 1 = 0

on comparing with the given equation in the question,

a = 1, b = 3, c = 3, d = 1

Therefore,

a+(b/c)+d = 3

So, the correct option is (b)

Hope this article was helpful.