Syllogisms appear in the DILR (Data Interpretation and Logical Reasoning) section of the CAT exam. However, sometimes, they also appear in the test’s VARC (Verbal Ability and Reading Comprehension) section. These concepts appear as 3-4 questions. Thus, they play an important role in defining your overall percentile. Consequently, a student must understand this topic well to score well.
Many students do not know what syllogism is or how to answer questions related to it. This article serves as a guide for all of your doubts related to CAT-level syllogism.
What are Syllogisms?
Syllogism is a word of Greek origin that means conclusion, conjecture, or inference. In the logical reasoning domain, Syllogism means a proposed argument. This argument is supported by two propositions. One proposition is the predicate of the conclusion, while the other is the subject of the conclusion. This conclusion is apparently drawn from the proposed argument, i.e., Syllogism. This, of course, sounds too confusing, doesn’t it?
Let’s understand what is what first. So, what exactly is a proposition?
A proposition is a statement that establishes a relation between two terms. Furthermore, this proposition has three components in its statement: subject, predicate, and relation.
Let’s take an example to understand this better.
- All papers are A4-sized
- All A4-sized papers are white
In the sentences given above, “papers” and “A4-sized papers” are the subjects of the statements. Meanwhile, the predicates of the statements are “A4-sized” and “white.”
By syllogism’s common definition, the above given example is apt. If you observe the above examples, you’ll notice the following:
- There’s no direct relation between the first statement’s subject and the second statement’s predicate.
- However, the predicate of the first statement becomes the subject of the second statement.
- Both of the statements use the word “All”
The above pattern is typical of syllogisms. Although the word “All” is used in both of the statements, this is not common practice. It mostly depends on the type of the proposition. So, the type in which ‘All’ is used is categorial proposition.
Types of Propositions
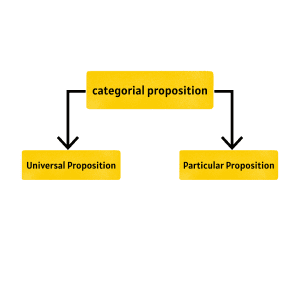
Categorial Propositions are further classified into two types: Universal proposition and Particular proposition.
1. Universal Proposition: These kinds of propositions either are completely inclusive or exclusive of a category or subject.
Example:
- No Indian uses chopsticks. (negative)
- All Koreans use chopsticks. (positive)
2. Particular Proposition: These kinds of proposition either partially include or exclude a category or subject.
- Some mangos are raw. (positive)
- Not all raw mangos are sour. (negative)
- Some mangos are not sweet. (negative)
Methods to Solve Syllogisms for CAT
There are two methods to solve syllogisms:
- The Venn Diagram Method
- The Analytical Method
The Venn Diagram Method
We all learned the concept of Venn Diagrams as part of set theory during our school days. However, if you still don’t remember them, Venn Diagrams are pictorial representations using circles or closed loops to represent mathematical or logical sets.
So, let’s first look into how Venn Diagrams represent different types of propositions.
| Types of Propositions | Universal/ Particular | Venn Diagram | Explanation |
| Positive | 1st type: All Y are Z. |  |
The statement says that All Y are Z. Thus, it implies that Y is a subset of Z, a superset. |
| Positive | 2nd type: Some Y are Z. |  |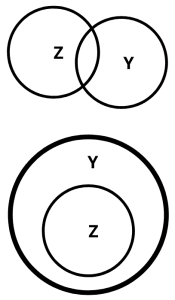
There are two scenarios here: either Set Y intersects with Set Z or Set Z is a subset of superset Y. |
| Negative | 3rd type : No Y are Z. |  |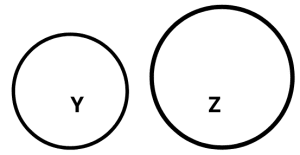
The statement states that no Y are Z. Therefore, Set of Y and Set of Z do not intersect at all. They remain apart as two separate sets. |
| Negative | 4th type:
Not all Y are Z; some Y are not Z. |
 |
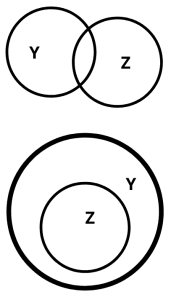Two scenarios are possible for this condition: either Set of Y and Set of Z intersect, or Set of Z is a subset of the superset of Y |
Using the above method, we can come to the following conclusions:
| Type of Proposition | The type of the proposition in the expectant conclusion | |||
| 1st type | 2nd type | 3rd type | 4th type | |
| 1st type | — | False | True | False |
| 2nd type | False | — | False | True |
| 3rd type | Not sure | False | — | Not sure |
| 4th type | False | Not sure | Not sure | — |
Example:
All pencils are erasers
All erasers are latex
Conclusion:
a. All latex are pencils
b. All pencils are latex
Options:
(a) Only conclusion a is true
(b) Only conclusion b is true
(c) Neither conclusion a nor b is true
(d) both conclusion a and conclusion b are true.
Approach:
1) Draw two separate Venn Diagrams of the statements.
2) Now, P = pencils and E = Erasers. So, as all pencils are erasers, it implies that P is a subset of Set E.
3) Then, L = latex. As all erasers are latex, E is a subset of the superset L.
In the end, we should get a figure as such:
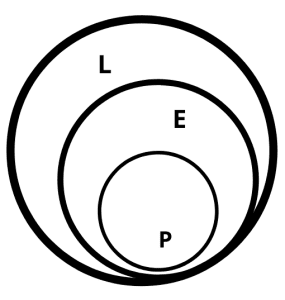
On analyzing the final Venn Diagram, we can say that only conclusion b follows. Therefore, the correct option is (b).
The Venn Diagram is practical and helps students avoid conclusions. Using this two-step Venn Diagram, you can easily solve any syllogism question. If you want to know more about this type of question, you can contact us at bellCAT.
The Analytical Method
Q. Some Indians are brown
All Indians are kind.
Approach:
1) Convert Statements so that the common term in both statements is the proposition’s predicate and the subject of the second statement.
The common term in the above propositions is Indians. So, let’s align Indians as the predicate of the first statement. The table below can be used to convert this.
| Type of Proposition | Type of the Proposition converted |
| 1st type | 3rd type |
| 2nd type | 2nd type |
| 3rd type | 3rd type |
| 4th type | Not possible to convert |
So, as the first statement is of type 2, it will be converted into type 2 . The converted statement is “Some browns are Indians”.
After aligning the statements:
Some browns are Indians.
All Indians are Kind.
2) Now, you can use the table below to draw conclusions after the conversion.
No conclusion combinations:
| The type of the first proposition | The type of the second proposition | The conclusion |
| 1st type | 3rd type | No conclusion |
| 1st type | 4th type | No conclusion |
| 2nd type | 2nd type | No conclusion |
| 2nd type | 4th type | No conclusion |
| 3rd type | 3rd type | No conclusion |
| 3rd type | 4th type | No conclusion |
| 4th type | 1st type or 2nd type or 3rd type | No conclusion |
Definite Conclusion Combinations:
| The type of the first proposition | The type of the second proposition | The conclusion |
| 1st type | 1st type | 1st type |
| 1st type | 2nd type | 2nd type |
| 2nd type | 1st type | 4th type* |
| 3rd type | 1st type | 3rd type |
| 2nd type | 3rd type | 4th type* |
| 3rd type | 2nd type | 4th type* |
Note*: The conclusion you get for type-4 when either type-2 and type-1 combine or type-2 or type-3 combine is opposite to the standard format of type-4.
Learn more like this with our latest strategies for CAT 2024 and experience the My Captain Program with a demo class. Also you can check about us from our website.
Author:
